CP-template-AND-interesting-problems
Trees Are Beautiful [Asia West Regional 2019] Problem Link
Problem

problem simplified:
Given a weighted tree. A tree is said to be Beautiful if the summation of all pair distance of the vertices of the tree is non-negative. If the given tree is not beautiful then we have to make it beautiful.
To make a tree beautiful, in each operation we can increase the weight of a negative edge by 1.
We have to print the minimum number of operation we need.
observations
- let define a word:
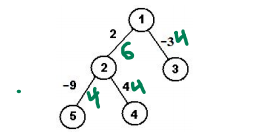
multiplication coefficientof an egde = number of time an edge is used to conect some pair of node in the tree. - If we increase the edge that has maximum multiplication coefficient, then it will be optimal.
multiplication coefficientfor each edge are written in thegreencolor below-
- If an edge has
lnode in one side andrnode on the the other side, thenmultiplication coefficient = l X r
Solution Idea
- First we will find any leaf node.
- Then we have to find
multiplication coefficientfor each edge. For doing this we need to run aDFSfrom aleaf node. - In that
DFSwe also count the summation of all pair distance of the vertices. - if summation is negative we need to do some operation. As we already know the
multiplication coefficientwe can easily iterate over the optimal edges and found out result.
Solution Code(C++)
#include <bits/stdc++.h>
using namespace std;
#define int long long int
#define ff first
#define ss second
int v_nm;
int isleaf[20005];
vector< pair<int,int> >grp[20005];
int tot;
vector< pair<int,int> >coeff;
void init(){
for(int i=0; i<=v_nm; i++){
isleaf[i] = 0; grp[i].clear();
}coeff.clear();
}
int dfs(int src,int p){
int nd = 0;
for(int i=0; i<grp[src].size(); i++){
int v = grp[src][i].ff;
int w = grp[src][i].ss;
if(p != v){
int lw = 1 + dfs(v, src);
int cof = lw * (v_nm-lw);
if(w < 0)
coeff.push_back( {(-cof), w});
tot += ((v_nm-lw)*lw)*w;
nd += lw;
}
}
return nd;
}
signed main() {
int t, cs = 1; cin>>t;
while(cs <= t){
cin>>v_nm;
for(int i=1; i<v_nm; i++){
int u, v, w; cin>>u>>v>>w;
grp[u].push_back({v,w});
grp[v].push_back({u,w});
isleaf[u]++; isleaf[v]++;
}
int lef = -1;
for(int i=0; i<=v_nm; i++){
if(isleaf[i] == 1){ lef = i; break; }
}
// multiplication coefficient off each eage
tot = 0;
dfs(lef, -1);
sort(coeff.begin(), coeff.end());
int op = 0;
for(int i=0; i<coeff.size(); i++){
if(tot >= 0) break;
int cf = -coeff[i].ff;
int w = -coeff[i].ss;
if((cf*w) <= abs(tot)){
tot += (cf*w);
op += w;
}else{
int x = (abs(tot) / cf);
if((abs(tot) % cf) != 0) x++;
tot += (x * cf);
op += x;
}
}
cout<<"Case "<<cs<<": "<<op<<endl;
init();
cs++;
}
}