CP-template-AND-interesting-problems
107 The Cat in the Hat Problem Link
problem simplified:
The problem is litte bit tricky. Let’s try to understand it by an example. But before that you must read the statement.
Let N = 3. Which means each cat will have 3 cats inside it.
And let, number of working cat = 9. Then the problem looks like the image below. Where red one is the initial cat. The red cat has 3 green cat inside it. Then each green cat has 3 orange cat inside them.
It is given that heigt of the initail cat is 1. So orange cat is of height 1.
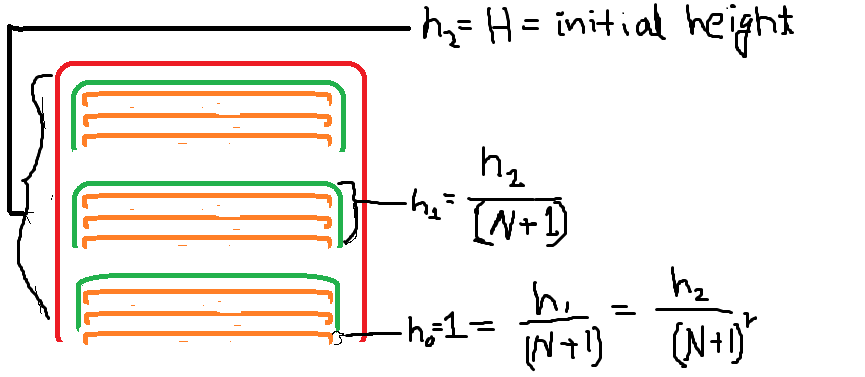
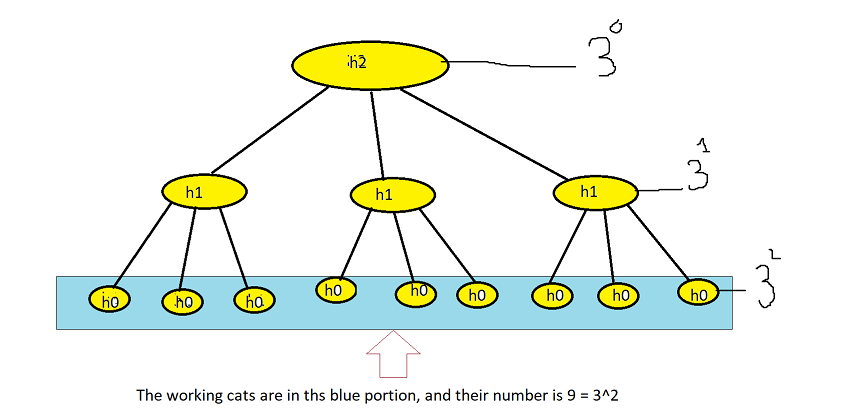
If you have any more confusion, you can look at this image below. This is a graph, and h2 is the initial cat and h0 are the working cats.
From the question we can have an equation, that is
h = H / (N+1)
=> H = h * (N+1) -----------(2)
working cat height h0 = 1
so using equation(2)
h1 = h0 * (N+1)
=> h1 = 1 * (N+1)
=> h1 = (N+1)
likely-
h2 = h1 * (N+1)
= (N+1) * (N+1)
= (N+1)^2
h3 = (N+1)^3
...............
...............
Hm = (N+1)^m [Here m is the (depth_of_graph-1). for the given image avobe m = 2]
So, we can say initial height, H = (N+1)^m —————–(a)
And, we can say number of working cat, WC = (N)^m ———–(b)
taking log in both side of the equation (a) and (b) we have -
log( (N+1)^m)/ log(N^m) = log(H) / log (WC)
=> log(N+1) / Log (N) = log(H) / log (WC)
=> ( log(N) / Log (N+1) )* log(H) = log (WC) --------------(c) Now we can `binary search` on equation (c), to find the value of N, as `H` and `WC` is given. <br> Then we can find `m` using equation (a) or (b). <br>
Now we have the height of the tree(m+1) and how many child each node have(N). So we can easily find the
number of cats that are not doing any work (cats of height greater than one) and also the sum of all
the cats heights.
observations
- You can’t binary serach on integer in this case, you must use floating number.
- If you give more time, you may find some O(n) solution of this problem.
Note: This code is little bit tricky: CP is all about smat thinking and determination.
Solution Code(C++)
#include <bits/stdc++.h>
#define lli long long int
using namespace std;
lli initial_hgt, working_cat;
int main() {
lli cs = 0;
while(++cs){
cin>>initial_hgt >>working_cat;
if(initial_hgt==0 && working_cat==0) break;
if (initial_hgt == 1){
printf ("0 1\n"); continue;
}
if (working_cat == 1){
lli x = 0, nwc;
while (1){
lli res = (1 << x) ;
if (res > initial_hgt){
nwc = x - 1; break;
}x++;
}
lli H = 0;
while ( initial_hgt >= 1 ){
H += initial_hgt;
initial_hgt /= 2;
}
printf ("%lld %lld\n", nwc , H); continue;
}
// log N / log N+1 = log working_cat / log initial_hgt
// (log N / log N+1) * log initial_hgt = log working_cat
long double l = 1, h = working_cat+1;
long double mid;
lli N = -1, m = -1;
for(lli i=0; i<500; i++){
mid = (l+h) / 2;
long double x = (log(mid*1.0) / log(mid+1.0)) * log(initial_hgt*1.0);
long double y = log(working_cat*1.0);
if(x < y){
l = mid;
}else if(x > y){
h = mid;
}
N = mid+.00000111;
}
m = 0;
lli wc = working_cat;
while(wc > 1){
wc /= N;
m++;
}
lli ht = 1, tot_cat = 0, tot_ht = 0;
for(lli i=m; i>=0; i--){
lli cat = pow(N,i);
tot_ht += cat * ht;
ht *= (N+1);
tot_cat += cat;
}
printf("%lld %lld\n",tot_cat-working_cat,tot_ht);
}
}