CP-template-AND-interesting-problems
11377 Airport Setup Problem Link
problem simplified:
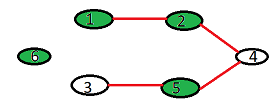

First image shows the test case given in the problem. Here green nodes are the nodes which has airport. And
edges(red color) connect pairs of node(flights path between pairs).
In this problem we can create new airport(make white node into green), but can’t create new flight path(new edge).
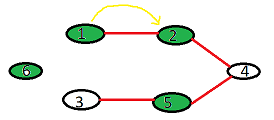
Image-2 shows the path from 1 to 2, and it’s cost is 0, as no white node are in the path.
Image-3 shows the path from 1 to 3, and it’s cost in 2, as two white nodes are in the path
And form node 1 to 6, the is no path, so result is -1.
Solution Idea
- We will give weight on the nodes. Green nodes are of weight 0 and white nodes are of weight 1.
- We are given two nodes x,y. To find the shortest path between them we will need simple dijkstra.
Solution Code(C++)
#include <bits/stdc++.h>
using namespace std;
#define inf 1<<30
vector<int>graph[2005];
bool has_airport[2005];
struct node{
int vrtx;
int wght;
node(int _vrtx,int _wght){
vrtx=_vrtx;
wght=_wght;
}
bool operator < (const node& p) const { return wght >p.wght;}
};
int vertxnum;
int edgenum;
int dist[100000];
int Dijaxtra(int src,int dst){
if(src == dst) return 0;
bool visit[100000];
for(int i=1;i<=vertxnum;i++){
dist[i]=inf;
visit[i]=false;
}
priority_queue< node >prq;
int w = has_airport[src] == true? 0 : 1;
prq.push(node(src,w));
dist[src]=0;
while(!prq.empty()){
node tp=prq.top();
prq.pop();
int W=tp.wght;
int V=tp.vrtx;
if(V == dst) return W;
if(visit[V]==true) continue;
visit[V] = true;
for(int i=0;i<graph[V].size();i++){
int u = graph[V][i];
int w = has_airport[u] == true? 0 : 1;
if(dist[u]>W+w){
dist[u]=w+W;
prq.push(node(u,w+W));
}
}
}
return -1;
}
void clear(){
for(int i=0; i<=vertxnum; i++){
has_airport[i] = false;
graph[i].clear();
}
}
int main() {
int t, cs = 1; cin>>t;
while(cs <= t){
int nd, eg, ap; cin>>nd >>eg >>ap;
vertxnum = nd, edgenum = eg;
for(int i=0; i<ap; i++){
int a; cin>>a;
has_airport[a] = true;
}
for(int i=0; i<eg; i++){
int u, v; cin>>u >>v;
graph[u].push_back(v);
graph[v].push_back(u);
}
cout<<"Case "<<cs<<":"<<endl;
int q; cin>>q;
while(q--){
int x, y; cin>>x >>y;
cout<<Dijaxtra(x,y)<<endl;
} cout<<endl;
clear();
cs++;
}
}